A História do Símbolo do Infinito
 Os Matemáticos estabeleceram a notação aparentemente críptica das fórmulas não como linguagem secreta, mas como maneira de aumentar a clareza. O símbolo de infinito é um dos primeiros exemplos disso.
Os Matemáticos estabeleceram a notação aparentemente críptica das fórmulas não como linguagem secreta, mas como maneira de aumentar a clareza. O símbolo de infinito é um dos primeiros exemplos disso.A literatura matemática de antigamente era, pelo menos à primeira vista, mais compreensível e acessível do que hoje, pois para descrever objetos matemáticos e suas relações, os autores utilizavam a linguagem escrita corriqueira e então.
A moderna linguagem de fórmulas, que impõe vários obstáculos intransponíveis para muitos leigos e, com isso, contribui para a pouca popularidade da disciplina, deve sua existência não a uma necessidade de proteção de segredos. Ao contrário, ela é assim pela necessidade de clareza. A história mostra que os símbolos surgiram para melhor formular hipóteses e argumentos, e com isso ganhar enfoques novos e mais precisos.
O século XVII representou um salto no desenvolvimento da matemática e das ciências naturais. Entre outras coisas, foi criado o cálculo diferencial e integral para tratar de problemas físicos concretos, relativos ao movimento e velocidades dos corpos. Na virada para o século XVIII, Isaac Newton (1643-1727) e Gottfried Wilhelm Leibniz (1646-1716) lançaram as bases de uma teoria sistemática. Essa evolução geral de conteúdo na matemática favoreceu o nascimento da linguagem de fórmulas.
O problema do infinito – seu significado para a matemática, a filosofia e a teologia – era debatido havia mais de 2 mil anos. Utilizada por Aristóteles, a palavra grega “aperion” já se destacava no tempo pré-socrático pela sua multiplicidade de significados. Ela queria dizer sem limites, incerto, absurdamente grande, e possuía também uma conotação negativa, correspondente ao caos do qual o mundo se formou. Aristóteles, de fato, via a infinitude como imperfeição. Foi somente no início da era cristã que se identificou o “infinito” ao “Um” divino.
As reflexões metafísicas da Idade Média, acerca da natureza do infinito e da essência do contínuo, prepararam o terreno para a abordagem matemática do cálculo infinitesimal no século XVII. Por exemplo, ao descartar os métodos dos antigos no cálculo de superfícies, comparar um círculo com um polígono de infinitos lados e calcular a superfície do círculo como soma de muitos triângulos, Johannes Kepler (1571-1630) tomou por base considerações filosófico-teológicas feitas por Nicolau de Cusa (1401-1464) a respeito do infinito real e potencial.
Em seus trabalhos matemáticos, John Wallis aprimorou métodos de Cavalieri. Depois da faculdade. Quando ainda não tinha nenhuma relação com a matemática, foi ordenado sacerdote em Londres. Durante esse tempo, colaborou para a fundação da Royal Society, e em 1643 ganhou um prêmio especial por sai participação na guerra civil como decifrador de mensagens secretas.
Quando Wallis se tornou professor da cadeira Savilian de geometria, na Universidade de Oxford, isso não aconteceu por reconhecimento de suas realizações matemáticas, mas como agradecimento por suas atividades políticas. No entanto, ele logo provou ter méritos para essa posição acadêmica. Até hoje é lembrado como precursor do cálculo infinitesimal e principal antecessor de Newton, o qual foi bastante influenciado por sua obra Arithmetica infinitirum, de 1656.
Antes, Wallis já escrevera um trabalho (De sectionibus conics, 1655) em que se distanciava da concepção matemática grega ao descrever as seções da esfera como curvas planas, às quais correspondiam equações algébricas. Deduziu então as propriedades dessas seções diretamente das equações, sem argumento geométrico. Participou, assim, de um dos desenvolvimentos centrais da história da matemática, a algebrização da geometria.
Foi nessa obra que Wallis introduziu, pela primeira vez, uma modificação nas considerações de Cavalieri. Enquanto as superfícies de Cavalieri se dividiam em uma quantidade infinita de pedaços, Wallis fala de uma superfície como a soma de um número infinito de paralelogramos de igual tamanho, e descreve esse tamanho como uma “parte infinitamente pequena, 1/∞ do tamanho total, e o símbolo ∞ representa o infinito”.
No transcorrer do século XIX, a teoria das grandezas infinitesimais foi definitivamente substituída pela moderna teoria do cálculo diferencial e integral, que passou a exigir, com base no estudo de conceitos como os de continuidade e convergência, um cuidado crescente com a exatidão formal e lógica. O símbolo ∞ indicava, como hoje, processos de passagem ao limite: ele descreve, no sentido de Aristóteles, um infinito potencial.
[1] Scientific American - Edição Especial nº 15: As diferentes faces do infinito



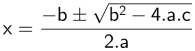
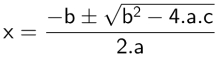
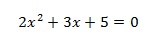
 (Delta), faz parte da formula de Bhaskara, sendo a raiz expressa na formula.
(Delta), faz parte da formula de Bhaskara, sendo a raiz expressa na formula.